Chapter 5, Section 5.4
Treatment of Lead Exposed Children Trial (TLC)
. use "tlc.dta"
. reshape long y, i(id) j(time)
(note: j = 0 1 4 6)
Data wide -> long
-----------------------------------------------------------------------------
Number of obs. 100 -> 400
Number of variables 6 -> 4
j variable (4 values) -> time
xij variables:
y0 y1 ... y6 -> y
-----------------------------------------------------------------------------
. tsset id time
panel variable: id (strongly balanced)
time variable: time, 0 to 6, but with gaps
delta: 1 unit
. label variable y "Blood Lead Level (mcg/dL)"
. label variable time "Time (in weeks)"
. ssc install xtgraph
checking xtgraph consistency and verifying not already installed...
installing into c:\ado\plus\...
installation complete.
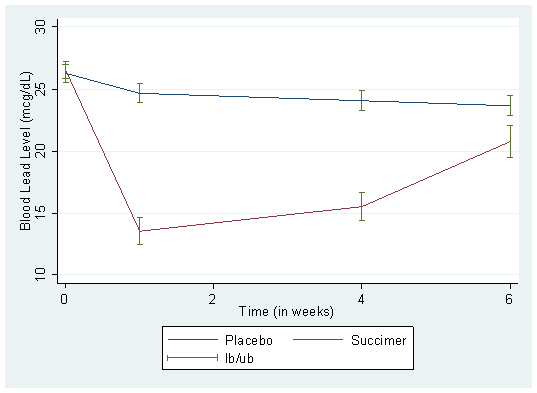
. xtgraph y, group(trt) av(mean) bar(se)
. xtmixed y i.trt##i.time || id: , noconst ///
residuals(unstructured, t(time)) reml
Obtaining starting values by EM:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = -1313.1276 (not concave)
Iteration 1: log restricted-likelihood = -1239.3532
Iteration 2: log restricted-likelihood = -1227.6607
Iteration 3: log restricted-likelihood = -1210.03
Iteration 4: log restricted-likelihood = -1208.0677
Iteration 5: log restricted-likelihood = -1208.038
Iteration 6: log restricted-likelihood = -1208.038
Computing standard errors:
Mixed-effects REML regression Number of obs = 400
Group variable: id Number of groups = 100
Obs per group: min = 4
avg = 4.0
max = 4
Wald chi2(7) = 296.50
Log restricted-likelihood = -1208.038 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
1.trt | .268 1.004503 0.27 0.790 -1.70079 2.23679
|
time |
1 | -1.612 .7919167 -2.04 0.042 -3.164128 -.0598719
4 | -2.202 .8149182 -2.70 0.007 -3.79921 -.6047895
6 | -2.626 .888521 -2.96 0.003 -4.367469 -.8845307
|
trt#time |
1 1 | -11.406 1.119939 -10.18 0.000 -13.60104 -9.210959
1 4 | -8.824 1.152468 -7.66 0.000 -11.0828 -6.565203
1 6 | -3.152 1.256559 -2.51 0.012 -5.614809 -.6891904
|
_cons | 26.272 .7102911 36.99 0.000 24.87985 27.66415
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
id: (empty) |
-----------------------------+------------------------------------------------
Residual: Unstructured |
sd(e0) | 5.022517 .3587505 4.366379 5.777253
sd(e1) | 6.659261 .4756592 5.789302 7.659948
sd(e4) | 6.883155 .4916517 5.983946 7.917487
sd(e6) | 7.658394 .5470263 6.657908 8.809223
corr(e0,e1) | .5712872 .0680466 .4230873 .6897174
corr(e0,e4) | .5698299 .0682146 .4213117 .688583
corr(e0,e6) | .5771983 .0673609 .4303008 .6943135
corr(e1,e4) | .7752546 .0403029 .6833543 .8429708
corr(e1,e6) | .5818712 .0668137 .4360169 .6979398
corr(e4,e6) | .5808796 .0669303 .4348027 .6971709
------------------------------------------------------------------------------
LR test vs. linear regression: chi2(9) = 210.18 Prob > chi2 = 0.0000
Note: The reported degrees of freedom assumes the null hypothesis is not on the
boundary of the parameter space. If this is not true, then the reported test is
conservative.
. test (i1.trt#i1.time) (i1.trt#i4.time) (i1.trt#i6.time)
( 1) [y]1.trt#1.time = 0
( 2) [y]1.trt#4.time = 0
( 3) [y]1.trt#6.time = 0
chi2( 3) = 107.79
Prob > chi2 = 0.0000