Chapter 19, Section 19.3
Study of Log C-Peptide Concentration in Children with Diabetes
. use "diabetes.dta"
. local i 1
. forvalues k=1(1)10 {
2. gen bf_`i'=cond(age - 4 - `k' > 0, age - 4 - `k', 0)
3. local ++i
4. }
. *Alternatively, use the mkspline command to create the 10 truncated line functions:
. *mkspline bf_0 5 bf_1 6 bf_2 7 bf_3 8 bf_4 9 bf_5 10 bf_6 11 bf_7 12 ///
bf_8 13 bf_9 14 bf_10 = age, marginal
. *drop bf_0
. xtmixed logc age || _all: bf_*, noconstant covariance(identity) reml
Performing EM optimization:
Performing gradient-based optimization:
Iteration 0: log restricted-likelihood = 53.57531
Iteration 1: log restricted-likelihood = 53.575431
Iteration 2: log restricted-likelihood = 53.575431
Computing standard errors:
Mixed-effects REML regression Number of obs = 43
Group variable: _all Number of groups = 1
Obs per group: min = 43
avg = 43.0
max = 43
Wald chi2(1) = 15.06
Log restricted-likelihood = 53.575431 Prob > chi2 = 0.0001
------------------------------------------------------------------------------
logc | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .0268907 .0069291 3.88 0.000 .0133099 .0404714
_cons | .5246127 .0317316 16.53 0.000 .4624198 .5868055
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]
-----------------------------+------------------------------------------------
_all: Identity |
sd(age_1..age_10)(1) | .0102037 .0062834 .003052 .0341134
-----------------------------+------------------------------------------------
sd(Residual) | .0554021 .0063124 .0443142 .0692644
------------------------------------------------------------------------------
LR test vs. linear regression: chibar2(01) = 5.52 Prob >= chibar2 = 0.0094
(1) bf_1 bf_2 bf_3 bf_4 bf_5 bf_6 bf_7 bf_8 bf_9 bf_10
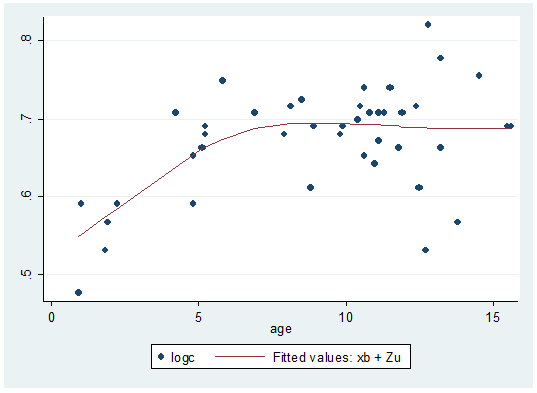
. predict yhat, fitted
. sort age
. graph twoway (scatter logc age)(line yhat age)